|

Posted on:
31 Jul 2014
|
The dynamic behaviour of a process can be abstracted to the point at which it can be represented by the smooth, continuous change of a series of state variables. This allows such a process to be represented mathematically as a set of DAEs.
The majority of processes, however, cannot be considered entirely continuous, but also experience significant discrete changes or discontinuities superimposed on their predominantly continuous behaviour. Such discrete changes, often referred to as events, can either be planned changes, called time events (for example, planned operational changes, such as start-up and shut-down, feed stock and/or product changes, process maintenance, switching a valve) or non-planned changes, called state events (overflow of a tank, (dis)appearance of a phase, inversion of a flow).
The exact time of occurrence of time events is either known a priori or it can be computed from the occurrence of a previous event. The time of occurrence of state events is not known in advance because it depends on the system fulfilling certain state conditions.
In addition to the two types of events we can classify events in another way, namely in events that do not change the (dynamic) model structure and events that change the (dynamic) model structure. With events that do not change the model structure, the balance equations are not altered, but some algebraic equations are changed. This usually results in a non-smooth continuation of the primary state variables.
———————————————————————————-
Example: Tank with Fast and Equilibrium Reaction Consider a tank with an inlet (consisting of two components A and B) and an outlet. The contents of the tank consist of four components (A, B, C and D) among which two fast reactions occur, namely:
A + B → C (1)
A ↔ D (2)
The first reaction (1) is a very fast, one way reaction. This means that there is no measurable inverse reaction and one of the two components A or B will always be completely consumed (i.e.: n_A =0 or n_B =0). The other reaction (2) is an equilibrium reaction, which means that there will always be a certain ratio between components A and D (c_A = k ∗ c_D). Because both reactions are fast in the context of the viewed time scale, the reaction terms that appear in the balance equations can be removed be using the Simple Index Reduction Algorithm (as discussed in previous blogs).
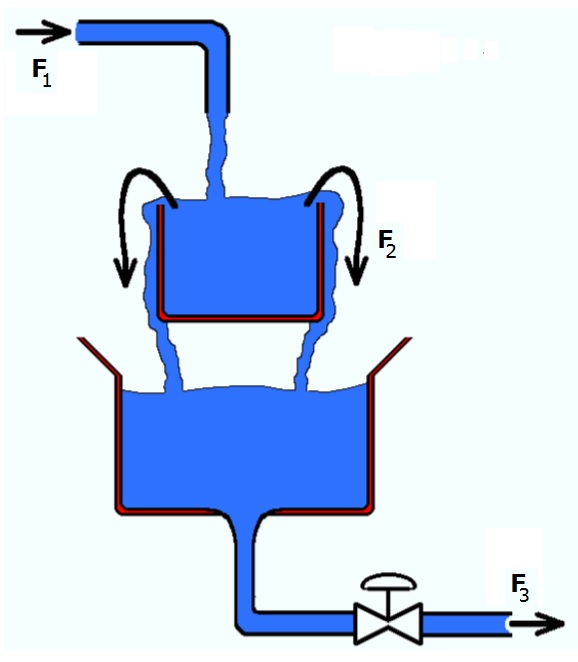
 The figure shows the result of a simulation of the tank. In this figure we can see three events taking place.
The figure shows the result of a simulation of the tank. In this figure we can see three events taking place.
At the start of the simulation there is an excess of A in the tank, which means that there will be no B, since all B that is available directly reacts with A to form C. The inlet flow contains more B than A and this results in diminishing quantities of A (and, consequently, D) in the tank until the amount of A (and D) in the tank reaches zero. At this point we encounter the first event, for now there will be an excess of B available in the tank and A (and D) will be non-existent.
At a certain point in time the input is changed such that the inlet flow will contain more A than B. A second event is the result. The amount of B will decrease until it reaches zero. This will initiate the third event, such that A (and D) will be present again.
Obviously, the first and last event were state events, while the second event was a time event.
———————————————————————————-
In our Modelling Methodology the model structure is typically never changed when an event occurs. Special IF-THEN-ELSE equations are used to describe state-dependent events. As an example, consider the overflow equation that was mentioned in our blog post on the Overflowing Tank:
F2: IF V > Vmax THEN
F2 = K * (V – Vmax)
ELSE
F2 = 0
END
Instead of changing the balance equations when there is no overflow (if the volume in the tank is lower than the maximum volume Vmax), the value of the overflow is simply set to zero.
For those who are interested in the simultaneous solving of (large) mathematical sets of differential and algebraic equations (DAE) that also include conditional statements (IF-THEN-ELSE type equations), it should be noted that the conditions are checked before a calculation step is performed. So, with the information of the previous time step it is determined which equations are used for solving the DAE. The effect of a state-dependent conditional statement is, therefore, typically “too late” if the calculation step is too large. This effect can give rise to “interesting” modelling results and should be well understood when making dynamic models. I will most likely discuss it in another blog post ;).
What is your experience with events and discontinuities in your models? Did you ever run into unexpected model behaviour because of these events?
I invite to post your experiences, insights and/or suggestions in the comment box below, such that we can all learn something from it.
To your success!
Mathieu.
———————————————–
The majority of processes, however, cannot be considered entirely continuous, but also experience significant discrete changes or discontinuities superimposed on their predominantly continuous behaviour. Such discrete changes, often referred to as events, can either be planned changes, called time events (for example, planned operational changes, such as start-up and shut-down, feed stock and/or product changes, process maintenance, switching a valve) or non-planned changes, called state events (overflow of a tank, (dis)appearance of a phase, inversion of a flow).
The exact time of occurrence of time events is either known a priori or it can be computed from the occurrence of a previous event. The time of occurrence of state events is not known in advance because it depends on the system fulfilling certain state conditions.
In addition to the two types of events we can classify events in another way, namely in events that do not change the (dynamic) model structure and events that change the (dynamic) model structure. With events that do not change the model structure, the balance equations are not altered, but some algebraic equations are changed. This usually results in a non-smooth continuation of the primary state variables.
———————————————————————————-
Example: Tank with Fast and Equilibrium Reaction Consider a tank with an inlet (consisting of two components A and B) and an outlet. The contents of the tank consist of four components (A, B, C and D) among which two fast reactions occur, namely:
A + B → C (1)
A ↔ D (2)
The first reaction (1) is a very fast, one way reaction. This means that there is no measurable inverse reaction and one of the two components A or B will always be completely consumed (i.e.: n_A =0 or n_B =0). The other reaction (2) is an equilibrium reaction, which means that there will always be a certain ratio between components A and D (c_A = k ∗ c_D). Because both reactions are fast in the context of the viewed time scale, the reaction terms that appear in the balance equations can be removed be using the Simple Index Reduction Algorithm (as discussed in previous blogs).

Figure: Simulation of a tank in which a fast and an equilibrium reaction take place.
At the start of the simulation there is an excess of A in the tank, which means that there will be no B, since all B that is available directly reacts with A to form C. The inlet flow contains more B than A and this results in diminishing quantities of A (and, consequently, D) in the tank until the amount of A (and D) in the tank reaches zero. At this point we encounter the first event, for now there will be an excess of B available in the tank and A (and D) will be non-existent.
At a certain point in time the input is changed such that the inlet flow will contain more A than B. A second event is the result. The amount of B will decrease until it reaches zero. This will initiate the third event, such that A (and D) will be present again.
Obviously, the first and last event were state events, while the second event was a time event.
———————————————————————————-
In our Modelling Methodology the model structure is typically never changed when an event occurs. Special IF-THEN-ELSE equations are used to describe state-dependent events. As an example, consider the overflow equation that was mentioned in our blog post on the Overflowing Tank:
F2: IF V > Vmax THEN
F2 = K * (V – Vmax)
ELSE
F2 = 0
END
Instead of changing the balance equations when there is no overflow (if the volume in the tank is lower than the maximum volume Vmax), the value of the overflow is simply set to zero.
For those who are interested in the simultaneous solving of (large) mathematical sets of differential and algebraic equations (DAE) that also include conditional statements (IF-THEN-ELSE type equations), it should be noted that the conditions are checked before a calculation step is performed. So, with the information of the previous time step it is determined which equations are used for solving the DAE. The effect of a state-dependent conditional statement is, therefore, typically “too late” if the calculation step is too large. This effect can give rise to “interesting” modelling results and should be well understood when making dynamic models. I will most likely discuss it in another blog post ;).
What is your experience with events and discontinuities in your models? Did you ever run into unexpected model behaviour because of these events?
I invite to post your experiences, insights and/or suggestions in the comment box below, such that we can all learn something from it.
To your success!
Mathieu.
———————————————–